1685. Земли Антарктиды
На карте Антарктики точками
изображено n полярных станций, каждая из
которых имеет натуральные координаты в прямоугольной сетке. Переход между двумя
станциями возможен, если расстояние между ними по прямой меньше двух единичных
отрезков карты. Станции, между которыми существует прямое или транзитное
соединение, объединяются в земли, причём каждая станция принадлежит только
одной земле.
Определите количество
арктических земель.
Вход.
В первой строке записано количество станций n, а в последующих n строках по два числа – координаты каждой из них. Все числовые значения
натуральные и не превышают 100.
Выход. Вывести количество
арктических земель.
|
Пример входа |
Пример выхода |
102 46 22 12 64 34 11 55 21 33 5 |
3 |
РЕШЕНИЕ
графы –
поиск в глубину
Анализ алгоритма
В двумерном массиве m создадим карту Антарктики: m[i][j]
= 1 если в позиции (i, j) находится
полярная станция и m[i][j] = 0 иначе.
На полученном
лабиринте ищем количество компонент связности. Из клетки можно двигаться в восьми
направлениях (по вертикали, по горизонтали и по диагоналям).
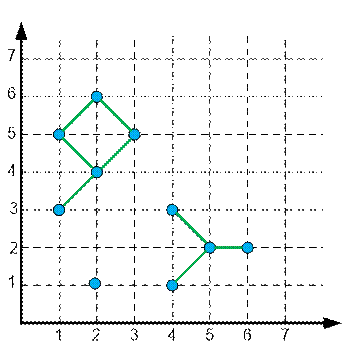
Пример
На
рисунке приведена карта Антарктики из примера. Карта содержит три компоненты
связности.
Реализация алгоритма
Объявим двумерный массив m, в котором будем
хранить карту
Антарктики.
#define MAX 101
int m[MAX][MAX];
Функция dfs совершает
поиск в глубину на прямоугольном лабиринте, стартуя с точки (i, j). Движение
производим во всех восьми направлениях.
void dfs(int i, int j)
{
if ((i < 0) || (j < 0)
|| (i >= MAX) || (j >= MAX)) return;
if (m[i][j] == 0) return;
m[i][j] = 0;
dfs(i + 1, j - 1); dfs(i + 1, j); dfs(i + 1, j + 1);
dfs(i, j - 1); dfs(i, j + 1);
dfs(i - 1, j - 1); dfs(i - 1, j); dfs(i - 1, j + 1);
}
Основная часть програмы. Читаем входные данные. Строим
лабиринт – карту Антарктики.
scanf("%d", &n);
for (i = 0;
i < n; i++)
{
scanf("%d %d", &a,
&b);
m[a][b] = 1;
}
В
переменной c подсчитываем количество арктических
земель.
c = 0;
Запускаем поиск в глубину на лабиринте. Перебираем
клетки двумерного массива и для каждой клетки с арктической станцией (для
которой m[i][j]
= 1) запускаем поиск в глубину dfs(i, j). С каждым запуском функции dfs увеличивается количество земель на 1.
for (i = 0;
i < MAX; i++)
for (j = 0;
j < MAX; j++)
if (m[i][j] == 1)
{
dfs(i, j);
c++;
}
Выводим ответ.
printf("%d\n", c);